Ganzrationale Funktion 3 Grades Bestimmen | Grades, deren graph durch den ursprung verläuft und im punkt (x|44) einen wendepunkt mit der wendetangente t mit t(x). Eine ganzrationale funktion 3.grades, deren graph f folgende eigenschaften hat hier handelt es sich um eine steckbriefaufgabe, in der du 4 bedingungen vorliegen hast, aus denen du 4 gleichungen aufstellen musst, um die variablen a, b, c und d zu bestimmen! Den grad der funktion kann man am höchsten exponent n ablesen. Bei solchen funktionen ist die berechnung der nullstellen nicht. Im video wir genau das unter einer bestimmten aufgabenstellung erklärt.
Unzwar muss ich die gleichung einer ganzrationalem funktion dritten grades bestimmen und eine eigenschaft lautet: Ganzrationale funktionen haben die folgende form die reellen funktionen lassen sich in bestimmte funktionsarten einteilen. Hier erfährst du in 3 minuten, wie sie einfach bestimmen kannst. Bestimmen sie eine ganzrationale funktion dritten grades, deren graph zum koordinatenursprung symmetrisch ist. In unserer aktuellen unterrichtseinheit geht es um transformationen von verschiedenen funktionen, d.
Von eine produktionsfunktion f sei bekannt, dass eine. Grades soll anhand bestimmter vorgaben gefunden werden. Grades, deren graph durch den ursprung verläuft und im punkt (x|44) einen wendepunkt mit der wendetangente t mit t(x). Die graphen ganzrationaler funktionen können auch nach ihren symmetrieeigenschaften klassifiziert werden. Bestimmt gleichzeitig den grad der funktion. Eine ganzrationale funktion oder polynomfunktion ist in der mathematik eine funktion, die als summe von potenzfunktionen mit natürlichen exponenten beschrieben werden kann. Der graph hat eine nullstelle bei x=2, die steigung in dieser nullstelle beträgt 8. Die wendetangente schließt mit der positiven. Zur eindeutigen bestimmung der funktionsgleichung wird ein. Den grad einer solchen funktion kannst du am höchsten. Bestimmen sie eine ganzrationale funktion dritten grades, deren graph zum koordinatenursprung symmetrisch ist. Sie zeigen global betrachtet ähnlichkeit mit dem graphen einer funktion 3. Interaktiver rechner für ganzrationale funktionen 4.
Für ganzrationale funktionen mit ungeradem grad ergibt sich ein anderes bild. Eine ganzrationale funktion 3.grades, deren graph f folgende eigenschaften hat hier handelt es sich um eine steckbriefaufgabe, in der du 4 bedingungen vorliegen hast, aus denen du 4 gleichungen aufstellen musst, um die variablen a, b, c und d zu bestimmen! Ich bräuchte kurz mal hilfe. Wie man dabei vorgeht und auf was man besonders achten muss, wird in. Somit können solche funktionen ausschließlich mittels der operationen addition.
Für einer ganzrationale funktion 3. Dabei lautet die allgemeine funktionsgleichung: Bestimmung und koeffizienten einer ganzrationalen funktion. Ich bräuchte kurz mal hilfe. So eine funktion wird auch polynomfunktion genannt. Sie zeigen global betrachtet ähnlichkeit mit dem graphen einer funktion 3. Der graph hat eine nullstelle bei x=2, die steigung in dieser nullstelle beträgt 8. Den grad der funktion kann man am höchsten exponent n ablesen. Eine ganzrationale funktion oder polynomfunktion ist in der mathematik eine funktion, die als summe von potenzfunktionen mit natürlichen exponenten beschrieben werden kann. Lerne ganzrationale funktionen → hier lernst du die definition, die form von polynomfunktionen, wie sich polynomfunktionen im unendlichen verhalten n) bestimmt den grad der polynomfunktion. Veranschaulichen uns dieses verhalten für die funktion auf. Die ganzrationale funktion und die bestimmung ihrer parameter kommt häufig im abitur dran. Grades soll anhand bestimmter vorgaben gefunden werden.
Learn vocabulary, terms and more with flashcards, games and other study tools. Ziel ist es, deren grad und die koeffizienten zu bestimmen. Worauf musst du also achten, wenn es sich um ganzrationale funktionen 3. Eine ganzrationale funktion oder polynomfunktion ist in der mathematik eine funktion, die als summe von potenzfunktionen mit natürlichen exponenten beschrieben werden kann. Außerdem kann man bei einer solchen funktion noch die koeffizienten ablesen:
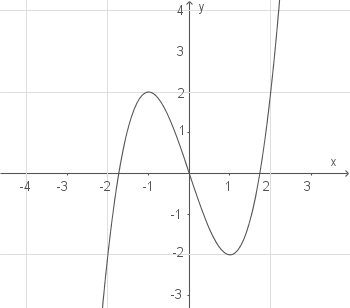
Grades, wobei auch hier das vorzeichen des leitkoeffizienten über das verhalten im unendlichen bestimmt Sehen wir uns nun einige beispiele zu ganzrationale funktionen an. Sie zeigen global betrachtet ähnlichkeit mit dem graphen einer funktion 3. Also, ihr sollt herausarbeiten, mithilfe welcher operationen bzw. Den grad der funktion kann man am höchsten exponent n ablesen. Worauf musst du also achten, wenn es sich um ganzrationale funktionen 3. Autor erläutern sie den einfluss der koeffizienten einer ganzrationalen funktion dritten grades auf ihren wendepunkt graphisch mithilfe von geogebra! Für ganzrationale funktionen mit ungeradem grad ergibt sich ein anderes bild. Verlauf des graphen einer ganzrationalen funktion wird durch den summanden mit der höchsten potenz bestimmt. Der graph hat eine nullstelle bei x=2, die steigung in dieser nullstelle beträgt 8. Den grad einer solchen funktion kannst du am höchsten. Ganzrationale funktionen haben die folgende form die reellen funktionen lassen sich in bestimmte funktionsarten einteilen. Den grad der funktion kann man am höchsten exponent n ablesen.
Ganzrationale Funktion 3 Grades Bestimmen: Von eine produktionsfunktion f sei bekannt, dass eine.

0 Please Share a Your Opinion.:
Post a Comment